vassle 101,&#EUng modulus.-Jagdiametral tröghetsmoment i axelsektionen,-k initm en momentstyvhet för en likvärdig länk som motsvarar helt öppen spricka. Ekvationen har två summor, 8211flexibilitet i samband med sprickor och flexibilitet för strålen utan sprickor.Den

 Det bör noteras att utan hänsyn till balens form, gränsförhållanden och sprickans position Bidrag till den allmänna balens flexibilitet beror endast på koefficienten k initmh ,Alltså den första summeringen. Medan strålen roterar, ändras flexibiliteten i sprickasektionen.Vi får följande:vassle 101, 

 g go&#flexibilitet för strålen utan spricka,  q)=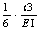 -kmNuvarande koefficient för ögonblickets styvhet för den givnaqNej. -Integrering av två ekvationer (5) och (7) får vivassle101,med beaktande av ekvationen (6) får vi lagen om förändring av ögonblickets styvhet beroende på skillnaden i fas

 e q 

 Okej.Den erhållna ögonblickstelheten hos en likvärdig länk beror endast på axelns diameter, materialegenskaper och sprickans djup.Förändring i sprickans läge i skaftet, axelns egenskaper inklusive stödenheterna ändrar inte ögonblickets styvhet i en likvärdig länk (på&#villkor att den del som innehåller crack förblir densamma i alla delar av sektionen med crack för vilka denerhållen).För att återgå till styvhetsmatrisen som erhållits tidigare kan dess styvhetskoefficienter skrivas som följande: vassle 

101, k

init 

 e , k  init 

 Åhh initiala värden för momentstyvhet vid motsvarande axlar för den fullständigt öppna sprickan&#Nej. Uppgiften att kinit e,kinit  -ÅhhBeräkningen kan lösas på två sätt.Den första är beräkning av ögonblicklig stelhet i FEM-programmet.Den andra är att använda teorin om fraktur mekanik.Det ger möjlighet att beräkna värden för koefficienter för lokal flexibilitet för öppen spricka om dess geometri, axelns diameter och materialegenskaper är kända [7,10].

 Algoritm för att simulera rotor system med crack Följande steg bör vidtas för att få koefficienter för sprickans momentstyvhet.1. Den fullständiga rotormodellen skapas i ett av de specialiserade programmen för analys av rotordynamik (förexempel, i Dynamics R4).2. Rotorsektionen med crack är markerad.  3. Sprickan delar axelsektionen i två delsystem.Länk som beskrivs av variabelns matriskoefficienter för styvhet[K (q) 

 , 

j)

av

Dimension 6x6 placeras mellan delsystem.

4. Ursprungliga koefficienter för ögonblickets styvhet

k

init

e ,kinitÅhhFör öppen spricka erhålls med de angivna metoderna.Ovanför.Dessa uppgifter är initiala för beräkning.Kompensmatriskoefficienter för länken som simulerar sprickan beräknas vid integrering av rörelseekvationer 

av rotorsystemet för varjeqNej.Med en icke-linjär fördelningsmatris som beskriver den icke-linjära dynamiska modellenRotorsystemet har följande egenskaper: vassle101,[m "

En matris av tröghetskoefficienter.

 [ C "

Matrix för dämpningskoefficienter och gyroskopkoefficienter.[K

" 

 matris av koefficienter för styvhet, (&#ör},(ör},(ör} Kolonner med vibrationsaccelerationer, vibrationshastigheter och vibrerande förskjutningar på motsvarande sätt.(-F(t)} &&alla Typer av dynamiska belastningar: interna och externa.En styvhetsmatris för en likvärdig länk kan delas in i två delar: konstant och variabel, och följande är sant:[&K Cingår i den allmänna styvhetsmatrisen för[K"System.Matris([q j] n,Kanvänds för att beräknareaktioner av en icke-linjär länk:-vassle101, 

 ör r , 

 ör r”smo”provrotationer av sektionerna runt motsvarande axlar.Den slutliga rörelseekvationen för systemet är följande:Okej.Den givna ekvationen kan lösas med numeriska metoder som RungeMetod Kutta, Newmark- metod etc.Lämpligheten hos den föreslagna algoritmen görs genom jämförelse av flexibiliteten hos de tvåStödstråle medcrack som erhålls i den begränsadeelement system och enligt den förmodade algoritmen i Dynamics R4.Uppgiften är att beräkna strålens deformation under enhetsstyrka i spricksektionerna för olika faser mellan spricka och kraft.Figur 3 visar resultaten av kontrollen av den föreslagna algoritmen.Tre resultat jämförs:Flexibilitet beräknas med hjälp av metoden med finish element (FEM).Radiell flexibilitet för modellen för strålen med spricka beräknas i FEM

System för hela området med vinkellägen för spricka.&#Flexibilitet beräknas med Dynamics R4, inledande data erhålls med FEM.Ursprungliga värden för ögonblicketstelhet för den fullt öppna sprickank inite, kinit

Åhherhålls som lösningsekvation (7) för

k-init

m-och radiell flexibilitet för strålen med spricka

gc-vid motsvarande riktning beräknas med hjälp av FEM.Moment styvhet för de mellanliggande vinkelsprickapositionerna ändras från lägsta till högsta nivå enligt (10-lagen).

Flexibilitet beräknas med Dynamics R4.Grundläggande data om momentflexibilitet för fullt öppen spricka

-k-e

 init , k-Åhh  

initerhålls analytiskt med hjälp av algoritmer för frakturmekanik [7, 10].Värdet av ögonblickflexibilitet förMellanliggande vinkelcrackpositioner ändras från lägsta till högsta nivå enligt lagen (10).Figur 3 Ändring av ljusets flexibilitet i cracksektom per revolution Resultaten av beräkningen av FEMModellen och modellerna i Dynamics R4 är nära varandra.Beräkningsresultaten med initiala förhållanden som erhållits analytiskt skiljer sig från FEM-resultaten mindre än 1%.Samtidigt beräknas den initiala styvheten analytiskt mycket snabbare än FEM-beräkningen och kräver mindre arbetstid och så lättaretillAnvändning.  Geometri och parametrar för rotor med spricka Geometri för rotorn med crack väljs för att visa att algoritmen fungerar till bästa möjliga fördel, tabell 1.Rotorn med den centrala skivan, stödet placeras vid axelns ändar.② ②②②

 ② ②-②②②②②②②②②  ② 

②

 ② ② ②-②-②-② 

②

 ② ② ②